线段树上二分
用形式化的语言讲,线段树上二分求解的是这一类问题。
给定 $L$,找到一个 $R \in [L,n]$ 满足$$f \Big( op\big([L,R-1]\big) \Big) = 1$$$$f\Big( op\big(R\big) \Big)=0$$
其中 $f$ 为某种合法性函数,$op$ 是将区间信息合并为 $f$ 能处理的信息的过程。
int query(int L,int& S,int x,int l,int r);其中 $S$ 为当前已经合并的区间信息,$x: [l,r]$ 为当前节点。
如何进行求解?既然要以 $L$ 为左端点进行区间合并,那么无论何时我们都优先递归左儿子,对于一个 $[l,r]$,若 $r<L$,就不再往下递归了。
此后便一定能找到 $L \le l$,且第一次找到时一定满足 $L=l$,于是就合并信息。如果此时 $f(S)=1$,那么往继续往右边找,结束递归。如果 $f(S)=0$ 且 $l=r$,答案 $R=l$。
如果 $l < L \operatorname{ and } L \le r$,往下递归即可。
借用严格鸽的图,不难看出合并区间的过程是连续的。按顺序合并了 $7,8,9,10,11$,在 $12$ 处找到了答案。
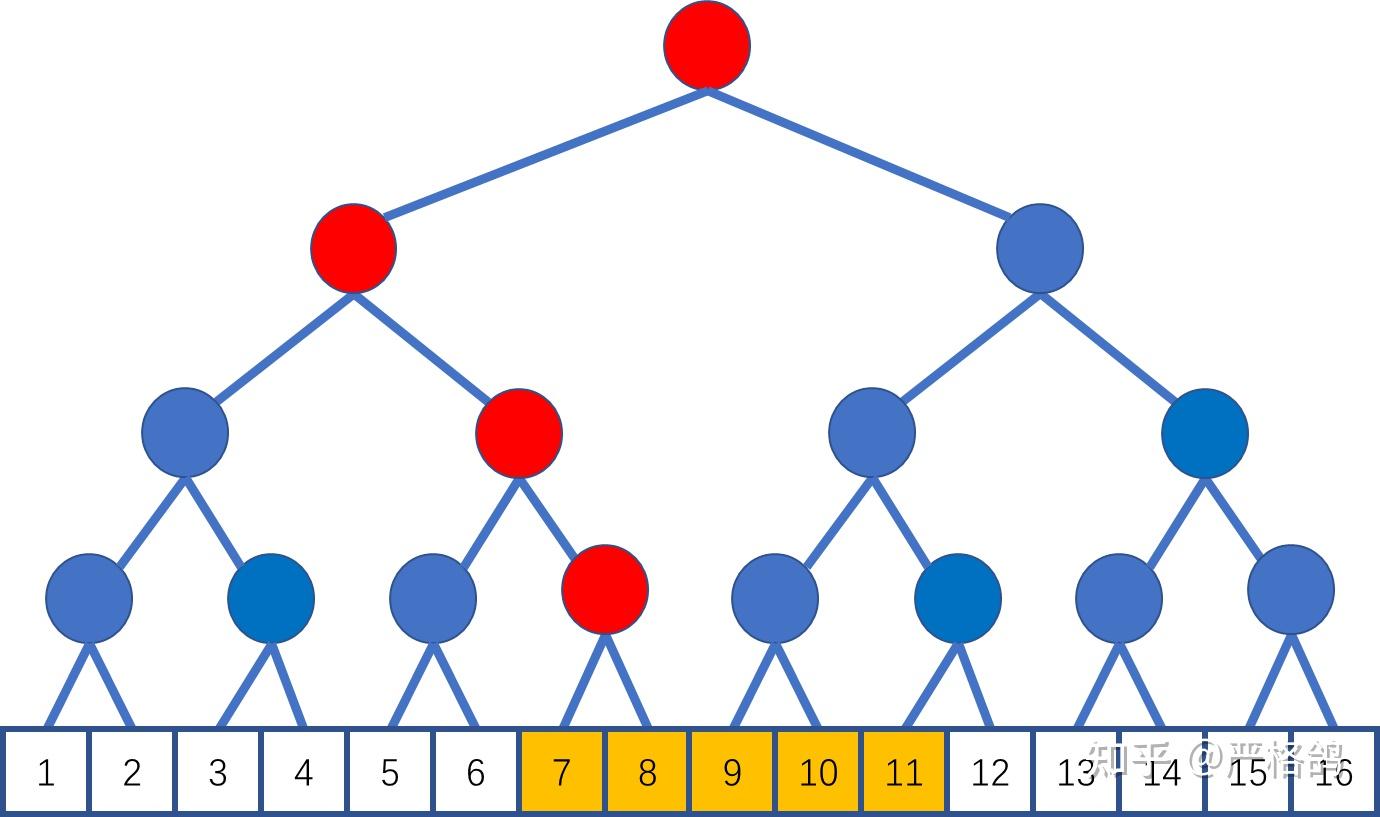
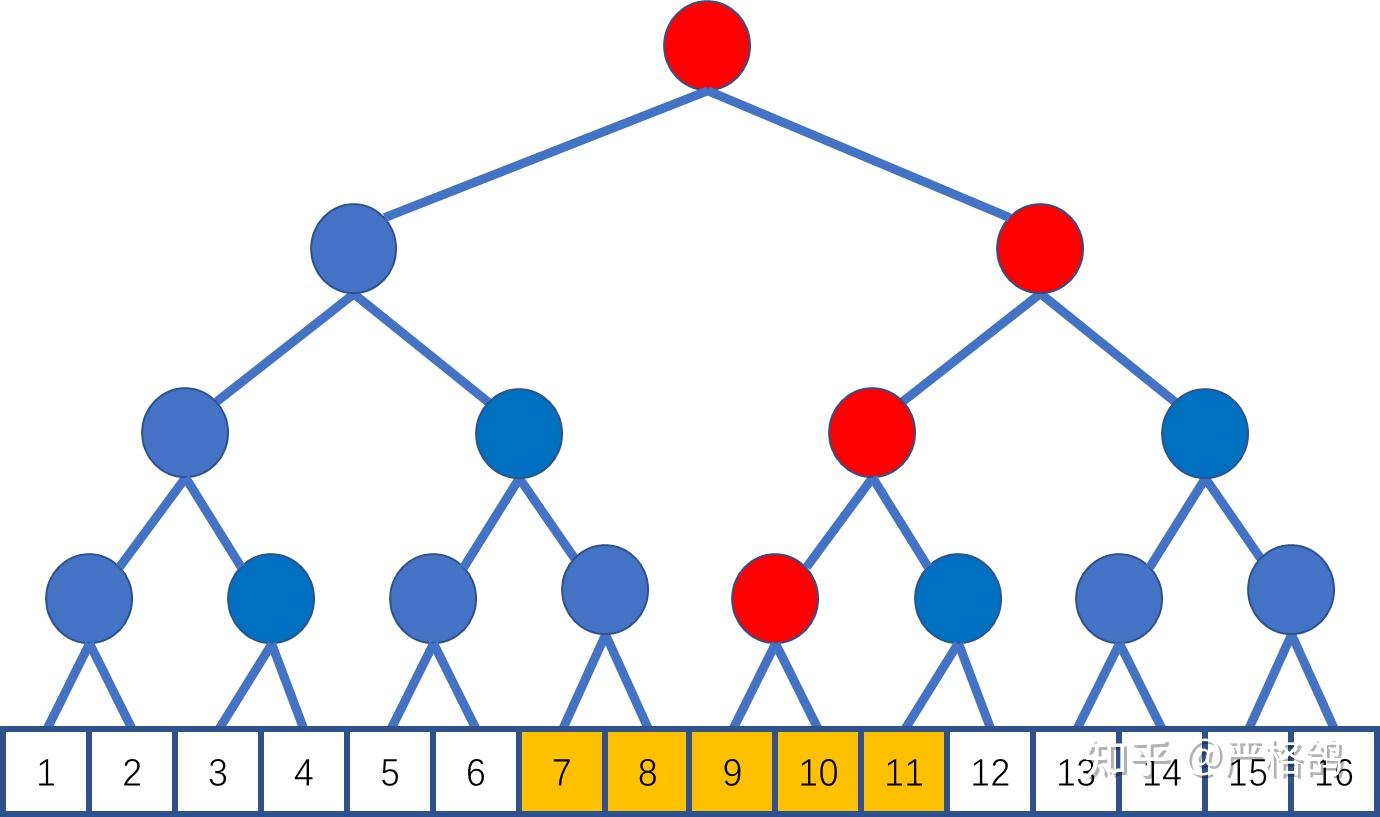
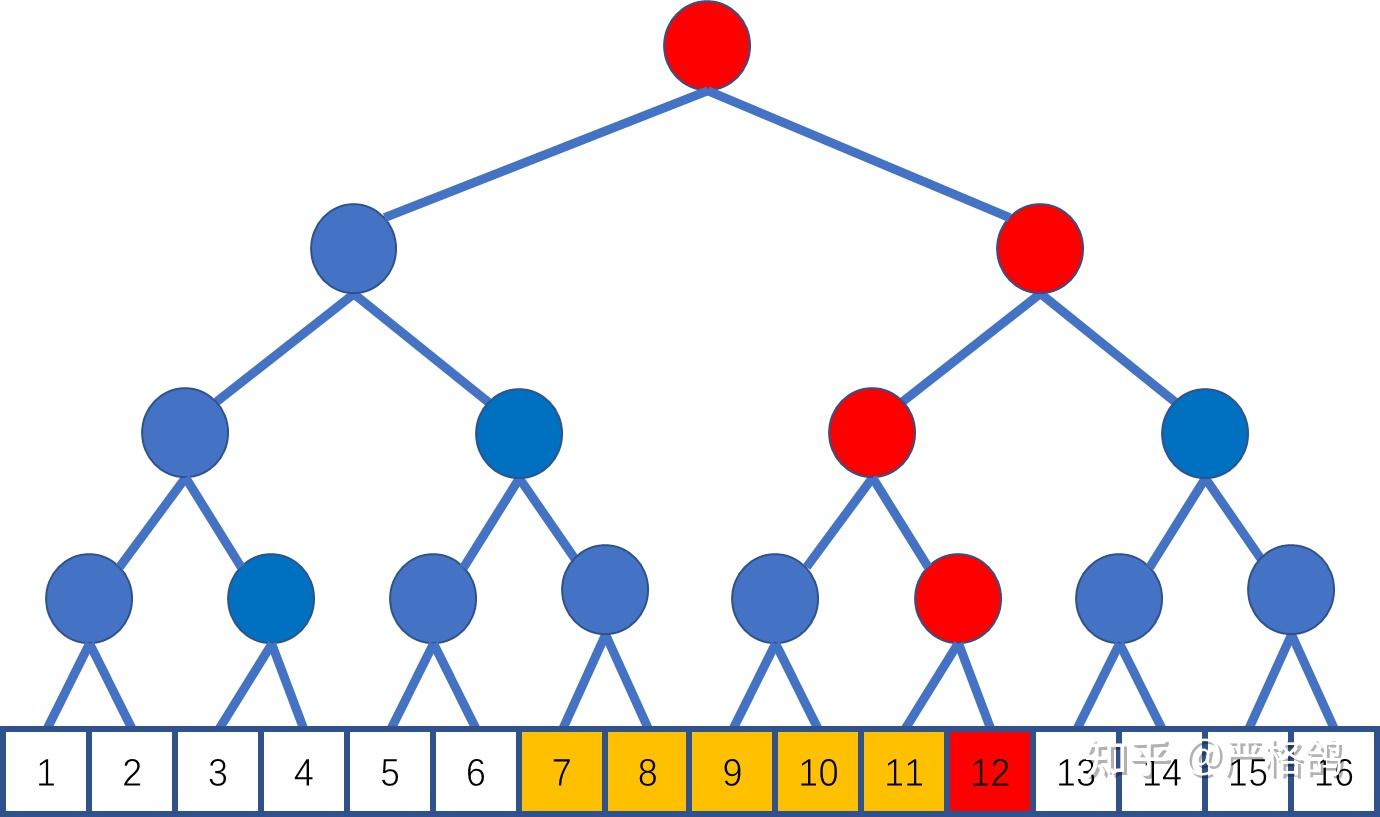
那这玩意复杂度是多少?
- 找 $L$ 的过程相当于优先递归左端点的单点查找,但是如果和 $[L,n]$ 无交便不会递归下去,复杂度 $O(\log_2 n)$。
- 之后只有合并后 $f$ 值为 $0$ 才往下递归,否则就合并信息。临界点又是固定的,所以每递归一次区间长度就减半,所以复杂度还是 $O(\log_2 n)$。
因此总复杂度 $O(\log_2n)$。
下面给出模板。
int query(int L,node& S,int x=1,int l=1,int r=n) {
if(r<L) return -1;
if(L<=l) {
if(f(op(S,x))) {
S=op(S,x);
return -1;
}
if(l==r) return l;
}
pushdown(x,l,r);
int mid=(l+r)>>1;
int res=query(L,S,x<<1,l,mid);
if(res==-1) return query(L,S,x<<1|1,mid+1,r);
return res;
}这种带着引用的写法存在一定局限性,但是某种程度上更加便于理解。
考虑这样一个模板题
维护一个 01 序列,求 $[L,n]$ 从左往右第 $k$ 个 1 的位置。
转化为
给定 $L$,找到 $R$ 满足 $[L,R-1]$ 中有不超过 $k$ 个 $1$。
因此node& S就是当前还需要找到 $S$ 个 $k$,op(S,x)就是 $S$ 减去区间内 $1$ 的个数,$f$ 就是看是不是大于 $0$(还要给 $R$ 留一个 1 的位置)。
这玩意的用法很灵活。
luogu4198 楼房重建
$n$ 点 $m$ 次操作,每次操作单点修改,操作完之后查询全局有多少 $a_i$,满足对于 $j \in [1,i-1]$,$a_j < a_i$。规模 $10^5$。
由于只查全局,所以考虑线段树直接维护。设 $s\big(x:[l,r]\big)$ 为 $[l,r]$ 内满足条件的 $a_i$ 的个数,$t\big(x:[l,r]\big)$ 为 $[l,r]$ 内的最大值。
对于一个区间 $x:[l,r]$,首先它会直接继承 $s(x)$,然后加上 $[mid+1,r]$ 中的一个子序列,满足严格递增且第一个元素大于 $t(x)$。
看起来不好做,但是考虑那第一个大于 $t(x)$ 的值,如果它在某个节点 $y$ 的左儿子内,那么其右儿子内大于它的数量一定是 $s(y)-s\big(lson(y)\big)$。
这样线段树上二分,在 $[mid+1,r]$ 内查找第一个大于 $t\big(lson(x)\big)$ 的数,顺便加上上面那个即可。
CF1440E Greedy Shopping
$n$ 个点 $m$ 次操作,一种操作是前缀取 $\max$,另一种操作是给定 $L$ 和 $k$,从 $L$ 到 $n$,如果到 $i$ 时有 $a_i \le k$,那么就让让答案加 1,$k-a_i$,表示购买。${a}$ 单调不增,规模 $2 \cdot 10^5$。
容易看出来购买的一定是若干个连续段。
单独求一个连续段是容易的,在 $[L,n]$ 上查找第一个满足 $Sum[L,i+1] > k$ 的 $i$ 即可。多个的话,可以再二分第一个小于等于剩下的 $k$ 的位置。
考虑一个性质,如果已经无法购买,说明剩下的 $k$ 不会多于之前的一半了,否则由于序列单调,必然可以购买,所以最多二分 $O(\log_2 \max{Y})$ 次。
然后记录区间最小值可以做到可行性剪枝。
考虑前缀取 $\max$ 的操作,区间内是有不同的数的,比较好的解决方法是记录区间最大值,只在取 $\max$ 的值不小于区间最大值时再打标记,pushup维护即可。
这玩意也能在权值线段树(主席树)上用。
动态开点
很多时候值域很大又不能离散化,为了降低空间复杂度,可以抛弃二叉树的结构,直接记录左右儿子,且一个节点被创建当且仅当被使用到。
如果是动态操作且值域较大,那么可以考虑动态开点。
那么如果一次操作复杂度是 $O(\log_2 n)$ 的话,用到的节点数也是 $O(\log_2n)$ 的,$m$ 次操作时候节点数量为 $O(m \log_2 n)$。
写法倒是很简单,而且能直接套上普通线段树的pushup和pushdown。
void modify(int& x,int p,int l=1,int r=n) {
if(x==0) x=++cnt;
if(l==r) {
ls[x]=rs[x]=0;
// init a node.
return;
}
int mid=(l+r)>>1;
if(p<=mid) modify(ls[x],p,l,mid);
else modify(rs[x],p,mid+1,r);
pushup(x);
}下面是摘自OI-wiki的两段代码。
// root 表示整棵线段树的根结点;cnt 表示当前结点个数
int n, cnt, root;
int sum[n * 2], ls[n * 2], rs[n * 2];
// 用法:update(root, 1, n, x, f); 其中 x 为待修改节点的编号
void update(int& p, int s, int t, int x, int f) { // 引用传参
if (!p) p = ++cnt; // 当结点为空时,创建一个新的结点
if (s == t) {
sum[p] += f;
return;
}
int m = s + ((t - s) >> 1);
if (x <= m)
update(ls[p], s, m, x, f);
else
update(rs[p], m + 1, t, x, f);
sum[p] = sum[ls[p]] + sum[rs[p]]; // pushup
}
// 用法:query(root, 1, n, l, r);
int query(int p, int s, int t, int l, int r) {
if (!p) return 0; // 如果结点为空,返回 0
if (s >= l && t <= r) return sum[p];
int m = s + ((t - s) >> 1), ans = 0;
if (l <= m) ans += query(ls[p], s, m, l, r);
if (r > m) ans += query(rs[p], m + 1, t, l, r);
return ans;
}没啥可说了。
线段树合并
两棵结构相同的线段树可以直接进行合并。
用两个指针 $p$ 和 $q$,同步遍历两棵树。
- 若 $p$ 或 $q$ 为空,那么非空的那个作为合并后的节点。
- 否则将 $q$ 的信息合并到 $p$,遍历左右儿子然后
pushup。
void merge(int& p,int q,int l=1,int r=n) {
if(!p||!q) { p|=q; return; }
if(l==r) {
// 合并叶子节点
return;
}
int mid=(l+r)>>1;
merge(ls[p],ls[q],l,mid);
merge(rs[p],rs[q],mid+1,r);
pushup(p);
}复杂度?
我不会证。


luogu3224 永无乡
板子题,并查集维护连通块,顺便进行合并,查询的时候全局线段树上二分即可。
luogu3201 梦幻布丁
每种颜色开一棵线段树,叶子为 $1$ 表示这个位置的颜色是它。那么这棵线段树对答案的贡献就是连续 $1$ 段的段数。记录区间左右端点的颜色,容易维护。
合并两种颜色就相当于合并这两棵线段树,对答案的影响显然与其它颜色段无关,随便搞一下就完了。
标记永久化
通过摒弃下传标记来降低常数。
- 遇到一个被完全覆盖的区间直接打标记
- 否则直接通过这个区间与操作区间的交修改区间信息
- 查询的时候加上标记
下面给出区间加法的代码。
void modify(int L,int R,int d,int x=1,int l=1,int r=n) {
if(L<=l&&r<=R) { tag[x]+=d; return; }
int mid=(l+r)>>1;
if(L<=mid) modify(L,R,d,x<<1,l,mid);
if(R>mid) modify(L,R,d,x<<1|1,mid+1,r);
pushup(x);
}
int query(int L,int R,int x=1,int l=1,int r=n) {
if(L<=l&&r<=R) return t[x]+tag[x]*(r-l+1);
int mid=(l+r)>>1, ans=tag[x]*(min(R,r)-max(L,l)+1);
if(L<=mid) ans+=query(L,R,x<<1,l,mid);
if(R>mid) ans+=query(L,R,x<<1|1,mid+1,r);
return ans;
}这不就是分块时维护的标记吗?
参考
《算法竞赛》 By 罗勇军,郭卫斌
《算法竞赛进阶指南》 By 李煜东