质数筛
埃氏筛模板
void prime() {
for(int i=2;i<=n;++i) if(!v[i]) {
for(int j=i*i;j<=n;j+=i) v[j]=1;
// 优化:从i*i开始枚举
}
}线性筛模板
void ora() {
for(int i=2;i<=n;++i) {
if(!v[i]) p[++cnt]=i;
for(int j=1;j<=cnt&&i*p[j]<=n;++j) {
v[i*p[j]]=1;
// p[j]是i*p[j]的最小质因子
if(i%p[j]==0) break;
}
}
}区间筛
求 $[a,b]$ 中的所有质数。
$a,b \le 10^{12}$,$b-a \le 10^6$。
由于每个合数 $x$ 存在至少一个 $\le \sqrt{x}$ 的质因数,所以先筛出 $[2,\sqrt{b}]$ 中的质数,用这些质数再筛掉 $[a,b]$ 中的合数。
luogu3601 签到题
区间筛筛欧拉函数,可作模板使用。
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define uint unsigned long long
#define PII pair<int,int>
#define MP make_pair
#define fi first
#define se second
#define pb push_back
#define eb emplace_back
#define SET(a,b) memset(a,b,sizeof(a))
#define CPY(a,b) memcpy(a,b,sizeof(b))
#define rep(i,j,k) for(int i=(j);i<=(k);++i)
#define per(i,j,k) for(int i=(j);i>=(k);--i)
int read() {
int a=0, f=1; char c=getchar();
while(!isdigit(c)) {
if(c=='-') f=-1;
c=getchar();
}
while(isdigit(c)) a=a*10+c-'0', c=getchar();
return a*f;
}
const int N=1e6+5, mod=666623333;
int l, r, phi[N], val[N];
int cnt, p[N];
bool v[N];
int cil(int x,int y) { return (x+y-1)/y; }
void haruhikage() {
for(int i=2;i*i<=r;++i) {
if(!v[i]) p[++cnt]=i;
for(int j=1;j<=cnt&&i*p[j]*i*p[j]<=r;++j) {
v[i*p[j]]=1;
if(i%p[j]==0) break;
}
}
}
void MyGO() {
rep(i,l,r) phi[i-l]=val[i-l]=i;
rep(i,1,cnt) {
for(int j=cil(l,p[i])*p[i];j<=r;j+=p[i]) if(val[j-l]%p[i]==0) {
phi[j-l]=phi[j-l]/p[i]*(p[i]-1);
while(val[j-l]%p[i]==0) {
val[j-l]/=p[i];
// printf("val[j-l]=%lld p[i]=%lld\n",val[j-l],p[i]);
}
}
}
rep(i,l,r) if(val[i-l]!=1) phi[i-l]=phi[i-l]/val[i-l]*(val[i-l]-1);
}
int hitoshizuku() {
int noroshi=0;
rep(i,l,r) (noroshi+=i-phi[i-l])%=mod;
return noroshi;
}
signed main() {
l=read(), r=read();
haruhikage();
MyGO();
printf("%lld\n",hitoshizuku());
return 0;
}约数相关
质因数分解
void divide() {
for(int i=2;i*i<=n;++i) if(n%i==0) {
p[++cnt]=i;
while(n%i==0) n/=i, ++e[cnt];
}
if(n>1) p[++cnt]=n, e[n]=1;
}时间复杂度 $O(\sqrt{n})$,常数好像小于 $\frac{1}{2}$。
还有 $O( \omega(n) )$ 的做法。先用筛法处理出每个数的最小质因子。分解 $n$ 时就可以 $O(1)$ 除掉一个质因子了 。
求约数集合
试除法
void fac() {
vector<int> factor;
for(int i=1;i*i<=n;++i) if(n%i==0) {
factor.push_back(i);
if(i*i!=n) factor.push_back(n/i);
}
}求单个数的约数集合,时间复杂度 $O(\sqrt{n})$。
倍数法
void fac() {
vector<int> factor[N];
for(int i=1;i<=n;++i) for(int j=1;i*j<=n;++j) {
factor[i*j].push_back(i);
}
}求 $[1,n]$ 中所有数的约数集合,时间复杂度 $O(n \log n)$。
约数个数函数
设 $n$ 分解后为 $\prod_{i=1}^m p_i^{e_i}$,则$$\sigma_0(n) = \prod_{i=1}^m (e_i+1)$$
从倍数法中能得到推论$$\sum_{i=1}^n \sigma_0 (i) = O(n \log n)$$
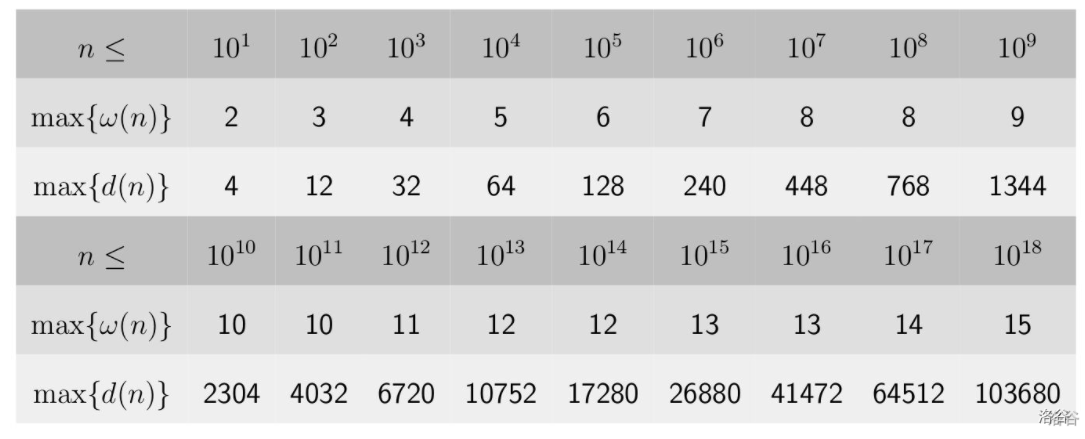
下图阐述了约数个数函数 $d(n) \text{ i.e. } \sigma_0(n)$ 以及质因数个数函数 $\omega(n)$ 在不同数量及下的最大值。
下图是有关 $d(n)$ 的一些估算技巧。

约数和函数
设 $n$ 分解后为 $\prod_{i=1}^{\omega(n)} p_i^{e_i}$,则 $$\begin{aligned}\sigma_1(n) &= \prod_{i=1}^{\omega(n)} \sum_{j=0}^{e_i} p_i^j\&= \prod_{i=1}^{\omega(n)} \frac{p_i^{e_i+1}-1}{p_i-1}\end{aligned}$$ 然而这个一般要在模 $P$ 意义下进行,$p_i-1$ 可能是模数的倍数,此时没有逆元。
不过由于此时 $p_i \bmod P = 1$,所以 $\sum_{j=0}^{e_i} p_i^j \equiv \sum_{j=0}^{e_i} 1^{j} \equiv e_i+1 \pmod {P}$,直接乘上即可。
还可以用分治法求 $\sum_{j=0}^{e_i} p_i^j$,设 $sum(a,b) =\sum_{i=0}^b a_i$。
若 $b$ 为奇数,记 $c=\lfloor\frac{b}{2}\rfloor$
$$
\begin{aligned} sum(a,b) &= \sum_{i=0}^{c} a^i + \sum_{i=c+1}^b a^i \\ &= \sum_{i=0}^c a_i + a^{c+1} \sum_{i=0}^c a^i \\ &= (1+a^{c+1}) \times sum(a,c) \end{aligned}
$$
若 $b$ 为偶数,记 $c=\frac{b}{2}$
$$
\begin{aligned}sum(a,b) &= \sum_{i=0}^{c-1} a^i + \sum_{i=c}^b a^i \\&= \sum_{i=0}^{c-1} a_i + a^{c} \sum_{i=0}^{c-1} a^i + a^b \\ &= (1+a^{c}) \times sum(a,c-1) + a^b\end{aligned}
$$
这样每次分治后,问题规模都会缩小一半,加上快速幂,复杂度 $O(\log b)$。
int sum(int a,int b) {
if(b==0) return 1;
if(b&1) return (1+fp(a,b/2+1))*sum(a,b/2)%mod;
else return ((1+fp(a,b/2+1))*sum(a,b/2-1)%mod+fp(a,b/2))%mod;
}GCD与LCM
定义与基本性质
int gcd(int x,int y) { return y? gcd(y,x%y):x; }
int lcm(int x,int y) { return x/gcd(x,y)*y; }$$
\operatorname{lcm}(x,y) = \frac{xy}{\gcd(x,y)}
$$
设长度为 $n$ 的序列 $a$,所有 $a_i$ 分解后的质因数总共有 $m$ 个,记为序列 $p$。设 $e_{i,j}$ 为 $a_j$ 分解后 $p_i$ 的指数。
记
$$
\alpha_i = \min_{j=1}^n \Big\langle e_{i,j} \Big\rangle
$$
$$
\beta_i = \max_{j=1}^n \Big\langle e_{i,j} \Big\rangle
$$
则
$$
\gcd_{i=1}^n (a_i) = \prod_{i=1}^m p_i ^{\alpha_i}
$$
$$
\text{lcm}{i=1}^n (a_i) = \prod{i=1}^m p_i^{\beta_i}
$$
$\gcd$ 与 $\operatorname{lcm}$ 满足结合律,可以用区间数据结构维护。
关于环
还是结合题目吧。
luogu6187 [NOI Online #1 提高组] 最小环
考虑这样一个东西,$x$ 在一个下标为 $[0,n-1]$ 的序列上跳,起点是 $0$,每次从 $i$ 跳到 $(i+L) \bmod n$,轨迹是个什么?
显然一定成环。
假设跳了 $k$ 次使得 $x$ 回到 $0$,那么一定有 $kL \bmod n =0$。
$kL$ 最小是 $\operatorname{lcm}(n,L)$,那么此时 $k = \frac{\operatorname{lcm}(n,L)}{L} = \frac{n}{\gcd(n,L)}$。
也就是说此时环上节点有 $\frac{n}{\gcd(n,L)}$ 个。
- 从不同的 $n$ 个点开始跳,总共形成 $n / k = \gcd(n,L)$ 个不同的环。
- 从 $0$ 开始跳,求经过的节点集。问题等价于 $kL \bmod n$ 有几个不同的值。可以转化为 $kL + pn = A$,对哪些 $A$ 有解,其中 $A \in [0,n-1]$。答案是当且仅当 $\gcd(n,L) \mid A$,因为只要有解,我们总能把 $k$ 调整成为一个正数。
回到本题上。
我们知道环长 $len=\frac{n}{\gcd(n,k)}$,直观地看,把最大的贪心塞进一个环里贡献最大。
结论:对于每一个环,都贪心选择剩余最大的 $len$ 个。设一个环内第 $i$ 大的数为 $p_i$,那么最优排列方式是 $p_1,p_3,p_5,\ldots$ 与 $p_2,p_4 ,\ldots$ 各形成两个半环,再将对应端点连接。
$\text{Proof by Elegia}$
首先我们讨论 $k=1$ 的答案。
我们考虑把乘积看成面积,那么第 $i$ 个点就在 $(a_i,a_i)$ 上,我们要最小化所有走路扫过的以端点形成的正方形面积之和。容易分析得到通过直线 $x=a_i$ 和 $y=a_j$ 切出来的每一个小矩形被经过的次数都达到了下界。
接下来考虑每个环长度为 $g$ 的情况,容易猜到我们将 $a_1 \sim a_g$ 放到第一个环里,$a_{g+1} \sim a_{2g}$ 放到第二个,以此类推。接下来简单证明一下:
- 注意到对于这个构造,如果加入一个 $\min \sim \max$ 之间的数,答案只会变小。
- 如果将 $\min$ 或者 $\max$ 删去,答案也会变小。
- 如果两个环的取值是交叉关系,设它们的值域是 $[l_1,r_1],[l_2,r_2]$,满足 $l_1 < l_2 < r_1 < r_2$,那么交换 $l_1,r_2$ 所属的值,显然每个环都加入了一个新的值,并去掉了极值。因此答案变小。
- 如果两个环的取值是包含关系,设值域是 $l_1 \le l_2 \le r_2 \le r_1$,那么这个方案甚至不如将这些数排在一个环里,因此这个方案必然不优。
根据以上四条,环必然是按顺序放置的。
这样单次还是 $O(n)$ 的。考虑到不同的环长只有 $\sigma_0(n)$ 种,因此记忆化即可。
复杂度 $O\Big(n \sigma_0(n)\Big)$。
// Problem: P6187 [NOI Online #1 提高组] 最小环
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P6187
// Author: yozora0908
// Memory Limit: 250 MB
// Time Limit: 2000 ms
//
// Let's Daze
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define uint unsigned long long
#define PII pair<int,int>
#define MP make_pair
#define fi first
#define se second
#define pb push_back
#define eb emplace_back
#define SET(a,b) memset(a,b,sizeof(a))
#define CPY(a,b) memcpy(a,b,sizeof(b))
#define rep(i,j,k) for(int i=(j);i<=(k);++i)
#define per(i,j,k) for(int i=(j);i>=(k);--i)
int read() {
int a=0, f=1; char c=getchar();
while(!isdigit(c)) {
if(c=='-') f=-1;
c=getchar();
}
while(isdigit(c)) a=a*10+c-'0', c=getchar();
return a*f;
}
const int N=2e5+5;
int n, m, ans0, a[N], rec[N];
signed main() {
n=read(), m=read();
rep(i,1,n) a[i]=read(), ans0+=a[i]*a[i];
sort(a+1,a+n+1,greater<int>());
while(m--) {
int k=read();
if(!k) {
printf("%lld\n",ans0);
continue;
}
int len=n/__gcd(n,k);
if(rec[len]) { printf("%lld\n",rec[len]); continue; }
int ans=0;
for(int i=1;i<=n;i+=len) {
for(int j=i;j+2<=i+len-1;j+=2) ans+=a[j]*a[j+2];
for(int j=i+1;j+2<=i+len-1;j+=2) ans+=a[j]*a[j+2];
ans+=a[i]*a[i+1]+a[i+len-1]*a[i+len-2];
}
printf("%lld\n",rec[len]=ans);
}
return 0;
}扩展欧几里得算法
Bézout定理
对于任意不全为 $0$ 的整数 $a,b$,存在无穷多对整数 $x,y$,满足 $ax + by = \gcd(a,b)$。
换言之,$a,b$ 的整系数线性组合得到的是所有 $\gcd(a,b)$ 的倍数。
模板
int exgcd(int a,int b,int& x,int& y) {
if(!b) { x=1, y=0; return a; }
int d=exgcd(b,a%b,y,x);
y-=a/b*x;
return d;
}求解不定方程与同余方程
对于不定方程 $ax+by = c$,其有整数解的充要条件是 $\gcd(a,b) \mid c$。
先用扩展欧几里得算法求出 $ax+by=\gcd(a,b)$ 的一组特解 $(x_0,y_0)$ 和 $d = \gcd(a,b)$。
$ax+by=c$ 的通解可以表示为$$\large \begin{cases}x= \frac{c}{d} x_0 + k \frac{b}{d} y=\frac{c}{d}y_0 - k \frac{a}{d}\end{cases}$$ 其中 $k \in \mathbb{Z}$。
那么对于线性同余方程$$ax \equiv b \pmod{p}$$可以转化为$$ax + py = b$$ 这里钦定 $b = \gcd(a,p)$。
用上述做法求出特解 $x_0$ 之后,所有与 $x_0$ 在模 $\frac{p}{\gcd(a,p)}$ 意义下同余的数构成的集合,就是这个方程的解集。
通过这一点可以得到最小正整数解。
void solve(int a,int b,int p) {
int x, y;
// b=gcd(a,b)
int d=exgcd(a,p,x,y);
p/=d;
x=(x%p+p)%p;
}同余相关
$$
a \bmod b = a - \lfloor \frac{a}{b} \rfloor \times b
$$
$$
a \times (b \bmod c) = ab \bmod ac
$$
$$
x \equiv y \pmod{p} \Longrightarrow xz \equiv yz \pmod{p}
$$
$$x \equiv y \pmod{p} \iff p \mid (x-y)$$
$$ax \equiv ay \pmod{p}$$
令 $d=\gcd(a,p)$,则$$x \equiv y \pmod{\frac{p}{d}}$$
费马小定理
若 $p$ 为质数,则对于任意整数 $a$,都有$$a^p \equiv a \pmod{p}$$
或者说,若 $p$ 为质数,$a,p$ 互质,那么$$a^{p-1} \equiv 1 \pmod{p}$$
威尔逊定理
若 $p$ 为质数,那么$$(p-1)! \equiv -1 \pmod{p}$$
乘法逆元
对于 $x \in [0,p)$,如果 $x$ 在模 $p$ 意义下的逆元存在,那么这个逆元唯一。
费马小定理
如果 $p$ 是质数,$a$ 不是 $p$ 的倍数,则$$a^{p-1} \equiv 1 \pmod{p}$$从而$$a \times a^{p-2} \equiv 1 \pmod{p}$$ $a^{p-2}$ 就是 $a$ 在模 $p$ 意义下的逆元。
复杂度 $O(\log_2 p)$。
扩展欧几里得算法
$$
ax \equiv 1 \pmod{p}
$$
等价于$${\exists} y, ax + py = 1$$ 这个不定方程有解的充要条件是 $\gcd(a,p)=1$,也就是 $a \bot p$。
求出的 $x_0$ 就是 $a$ 在模 $p$ 意义下的逆元。
复杂度 $O(\log_2 p)$。
递推逆元
void getinv() {
inv[0]=inv[1]=1;
for(int i=2;i<=n;++i) inv[i]=(p-p/i)*inv[p%i]%p;
}复杂度 $O(n)$。
求阶乘逆元
void getinv() {
inv[0]=1;
inv[n]=fp(fac[n],p-2);
for(int i=n-1;i;--i) inv[i]=inv[i+1]*(i+1)%p;
}复杂度 $O(n+\log_2 p)$
整除分块
$$
\sum_{i=1}^n \Big \lfloor \frac{n}{i} \Big\rfloor
$$
只有 $O(\sqrt{n})$ 种不同的值,且每一种值对应的 $i$ 连续。
void block() {
for(int l=1,r=0;l<=n;l=r+1) {
r=n/(n/l);
// 值为n/l的区间是[l,r]
}
}欧拉函数
定义
$\varphi(n)$ 表示 $[1,n]$ 中与 $n$ 互质的数的个数。
设 $n$ 分解后为 $\prod_{i=1}^m p_i^{e_i}$,则$$\varphi(n) = n \prod_{i=1}^m (1-\frac{1}{p_i})$$ 所以可以在分解质因数的过程中计算欧拉函数,复杂度 $O(\sqrt{n})$。
void getphi(int n) {
int phi=n;
for(int i=2;i*i<=n;++i) if(n%i==0) {
phi=phi/i*(i-1);
while(n%i==0) n/=i;
}
if(n>1) phi=phi/n*(n-1);
}可以用线性筛在 $O(n)$ 的时间里求出 $[1,n]$ 所有数的欧拉函数。
void getphi() {
for(int i=2;i<=n;++i) {
if(!v[i]) v[i]=1, p[++cnt]=i, phi[i]=i-1;
for(int j=1;j<=cnt&&i*p[j]<=n;++j) {
v[i*p[j]]=1;
// p[j]是i*p[j]的最小质因子
if(i%p[j]==0) {
phi[i*p[j]]=phi[i]*p[j];
break;
}
phi[i*p[j]]=phi[i]*phi[p[j]];
}
}
}性质
积性函数。$$a \bot b \Longrightarrow \varphi(ab) = \varphi(a)\varphi(b)$$
$$
\sum_{d \mid n} \varphi(d) = n
$$
$$
\sum_{i=1}^n [\gcd(i,n)=1]i = \frac{n \times \varphi(n)}{2}
$$
另外线性筛求欧拉函数的过程中用了两个性质。
- 若 $p$ 为质数,$p \mid n$,但 $p^2 \nmid n$,那么 $\varphi(n)=\varphi(n/p) \times \varphi(p)$。
- 若 $p$ 为质数,$p \mid n$,且 $p^2 \mid n$,那么 $\varphi(n)= \varphi(n/p) \times p$。
欧拉定理
若 $a \bot n$,则$$a^{\varphi(n)} \equiv 1 \pmod{n}$$
另外有结论,若 $a \bot n$,那么满足$$a^x \equiv 1 \pmod{n}$$ 最小的 $x$ 一定是 $\varphi(n)$ 的约数。
扩展欧拉定理
懒得打公式了。

进制转换
将 $n$ 位 $a$ 进制数转化为 $m$ 位 $b$ 进制数的做法如下。
如果这个十进制数存的下的话,
- 将给定的 $a$ 进制数从高位到低位扫一边,每次将当前结果乘 $a$ 再加上当前位的系数,这样就能转化成 $10$ 进制。
- 从 $10$ 进制转化为 $b$ 进制。先模再除,取最低位放进去,重复这个过程。
复杂度是 $O(n)$ 的。
exCRT
CRT 完全可以被 exCRT 代替。
线性筛求常见积性函数
莫比乌斯函数

欧拉函数

约数个数函数
